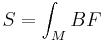Topological quantum field theory

A topological quantum field theory (or topological field theory or TQFT) is a quantum field theory which computes topological invariants.

Although TQFTs were invented by physicists, they are also of mathematical interest, being related to, among other things, knot theory and the theory of four-manifolds in algebraic topology, and to the theory of moduli spaces in algebraic geometry. Donaldson, Jones, Witten, and Kontsevich have all won Fields Medals for work related to topological field theory.

In condensed matter physics, topological quantum field theories are the low energy effective theories of topologically ordered states, such as fractional quantum Hall states, string-net condensed states, and other strongly correlated quantum liquid states.

Contents

Overview

In a topological field theory, the correlation functions do not depend on the metric of spacetime. This means that the theory is not sensitive to changes in the shape of spacetime; if the spacetime warps or contracts, the correlation functions do not change. Consequently, they are topological invariants.

Topological field theories are not very interesting on the flat Minkowski spacetime used in particle physics. Minkowski space can be contracted to a point, so a TQFT on Minkowski space computes only trivial topological invariants. Consequently, TQFTs are usually studied on curved spacetimes, such as, for example, Riemann surfaces. Most of the known topological field theories are defined on spacetimes of dimension less than five. It seems that a few higher dimensional theories exist, but they are not very well understood.

Quantum gravity is believed to be background-independent (in some suitable sense), and TQFTs provide examples of background independent quantum field theories. This has prompted ongoing theoretical investigation of this class of models.

(Caveat: It is often said that TQFTs have only finitely many degrees of freedom. This is not a fundamental property. It happens to be true in most of the examples that physicists and mathematicians study, but it is not necessary. A topological sigma model with target infinite-dimensional projective space, if such a thing could be defined, would have countably infinitely many degrees of freedom.)

Specific models

The known topological field theories fall into two general classes: Schwarz-type TQFTs and Witten-type TQFTs. Witten TQFTs are also sometimes referred to as cohomological field theories.

Schwarz-type TQFTs

In Schwarz-type TQFTs, the correlation functions computed by the path integral are topological invariants because the path integral measure and the quantum field observables are explicitly independent of the metric. For instance, in the BF model, the spacetime is a two-dimensional manifold M, the observables are constructed from a two-form F, an auxiliary scalar B, and their derivatives. The action (which determines the path integral) is

S=\int_M B F\,

The spacetime metric does not appear anywhere in this theory, so the theory is explicitly topologically invariant. Another, more famous example is Chern-Simons theory, which can be used to compute knot invariants.

Witten-type TQFTs

In Witten-type topological field theories, the topological invariance is more subtle. For example the Lagrangian for the WZW model does depend explicitly on the metric, but one shows by calculation that the expectation value of the partition function and a special class of correlation functions are in fact diffeomorphism invariant.

Mathematical formulations

Atiyah-Segal axioms

Atiyah suggested a set of axioms for topological quantum field theory which was inspired by Segal's proposed axioms for conformal field theory, (Atiyah 1988). These axioms have been relatively useful for mathematical treatments of Schwarz-type QFTs, although it isn't clear that they capture the whole structure of Witten-type QFTs. The basic idea is that a TQFT is a functor from a certain category of cobordisms to the category of vector spaces.

There are in fact two different sets of axioms which could reasonably be called the Atiyah axioms. These axioms differ basically in whether or not they study a TQFT defined on a single fixed n-dimensional Riemannian / Lorentzian spacetime M or a TQFT defined on all n-dimensional spacetimes at once.

[ed. What follows is still in rough draft form and should be regarded suspiciously.]

The case of a fixed spacetime

Let 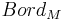Bord_M be the category whose morphisms are n-dimensional submanifolds of M and whose objects are connected components of the boundaries of such submanifolds. Regard two morphisms as equivalent if they are homotopic via submanifolds of M, and so form the quotient category 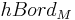hBord_M: The objects in 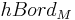hBord_M are the objects of 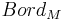Bord_M, and the morphisms of 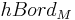hBord_M are homotopy equivalence classes of morphisms in 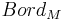Bord_M. A TQFT on M is a symmetric monoidal functor from 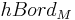hBord_M to the category of vector spaces.

Note that cobordisms can, if their boundaries match up, be sewn together to form a new bordism. This is the composition law for morphisms in the cobordism category. Since functors are required to preserve composition, this says that the linear map corresponding to a sewn together morphism is just the composition of the linear map for each piece.

There is an equivalence of categories between the category of 2-dimensional topological quantum field theories and the category of commutative Frobenius algebras.

All n-dimensional spacetimes at once

To consider all spacetimes at once, it is necessary to replace 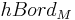hBord_M by a larger category. So let 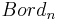Bord_n be the category of bordisms, i.e. the category whose morphisms are n-dimensional manifolds with boundary, and whose objects are the connected components of the boundaries of n-dimensional manifolds. (Note that any 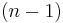(n-1)-dimensional manifold may appear as an object in 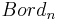Bord_n.) As above, regard two morphisms in 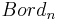Bord_n as equivalent if they are homotopic, and form the quotient category 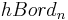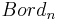hBord_n. Bord_n is a monoidal category under the operation which takes two bordisms to the bordism made from their disjoint union. A TQFT on n-dimensional manifolds is then a functor from 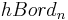hBord_n to the category of vector spaces, which takes disjoint unions of bordisms to the tensor product f [ed. unfinished]

For example, for (1+1)-dimensional bordisms (2-dimensional bordisms between 1-dimensional manifolds), the map associated with a pair of pants gives a product or coproduct, depending on how the boundary components are grouped – which is commutative or cocommutative, while the map associated with a disk gives a counit (trace) or unit (scalars), depending on grouping of boundary, and thus (1+1)-dimension TQFTs correspond to Frobenius algebras.

Generalizations

For some applications, it is convenient to demand extra topological structure on the morphisms, such as a choice of orientation.

See also

References

Schwarz' original paper introducing the ideas of TQFT's, in which he produces a Ray-Singer invariant from a QFT functional:

Quantum field theories
Standard
Four-fermion interactions